2011년06월13일 6번
[과목 구분 없음] 거리측량을 스틸테이프로 측정할 때 1회 측정시 2mm의 정오차와 2mm의 우연오차가 생긴다면 전체거리(L)를 n구간(회)으로 나누어 측정했을 경우 전체거리에 대한 확률 오차는?
-
①
-
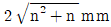
②
-
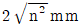
③
-
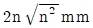
④
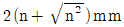
(정답률: 81%)
문제 해설
전체거리(L)를 n구간으로 나누어 측정할 경우, 각 구간의 길이는 L/n이 된다. 따라서 각 구간에서의 정오차와 우연오차는 각각 2mm/n과 2mm/n√3이 된다. 이를 이용하여 전체거리에 대한 확률 오차를 계산하면 다음과 같다.
확률오차 = √(n(정오차)^2 + n(우연오차)^2)
= √(n(2/n)^2 + n(2/√3n)^2)
= √(4/n + 4/3n)
= 2√(1/n + 1/3n)
따라서, n이 커질수록 확률 오차는 작아진다. 이를 그래프로 나타내면 "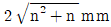"와 같이 n이 증가함에 따라 확률 오차가 감소하는 것을 확인할 수 있다.
확률오차 = √(n(정오차)^2 + n(우연오차)^2)
= √(n(2/n)^2 + n(2/√3n)^2)
= √(4/n + 4/3n)
= 2√(1/n + 1/3n)
따라서, n이 커질수록 확률 오차는 작아진다. 이를 그래프로 나타내면 "
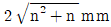"와 같이 n이 증가함에 따라 확률 오차가 감소하는 것을 확인할 수 있다.
